French
French
 German
German
 Italian
Italian
 Spanish
Spanish
 Portuguese
Portuguese
 Japanese
Japanese
 Korean
Korean
 Chinese
Chinese
FormulaOne Programmer's Manual
This file documents the use of the Formula One compiler.
Copyright © 2003, 2004, 2005, 2006, 2007, 2008, 2009 K2 Software Corp.
About This Document
Preface
What Is Formula One
FormulaOne and Other Languages
Formulas and Queries
Predicates
Data Types
Modes
Control Structures
Procedures, Subroutines and Functions
Building Types
Database Files
Collecting Solutions with "all"
Miscellaneous Advanced Topics
Queries
FormulaOne Language Definition
BNF Syntax of FormulaOne
Type Conversion
Mode Coercion
Constraints
Runtime Library
This file documents the use of the FormulaOne compiler. The screenshots in this document are based on the FormulaOne Release 40 IDE (Integrated Development Environment).
Other releases may have different look and feel and a different method of invoking queries. This should be rather irrelevent, as this document focuses on the programming language itself.
Installation of the FormulaOne Compiler Release 40 also installs the Tutorial project with the module called Tutorial. It
contains most of the predicates discussed in this manual. You can use this module if you do not plan to type the
predicates yourself. The module must be compiled before it can be used. Once the module is compiled it can be used by various queries
without a recompilation, unless, of course, it has been modified.
FormulaOne a language which integrates procedural, declarative and database programming into one
highly efficient language.
Since the early 1980's micro-computers have won an important place in science, education, entertainment and industry.
Procedural programming,
which details how computing is performed, has lighten the drudgery of repetitive calculation for many people.
However, procedural programming
shows weakness when faced with problems concerning logic, reasoning or the evaluation of complex data relations.
One answer to this impasse is declarative programming, which lies at the very heart of AI (artificial intelligence).
Using this approach, the relation between information and objects is the matter of scrutiny and many of the programming
details can be left to the compiler.
With declarative programming, the inference engine organizes information and then finds a way to logically interpret or process that information,
when queried with respect to a given problem.
Expert systems place exceptional demands on such information processing, and great programming effort must be
expended to meet the challenge when using procedural languages such as C, Fortran or Pascal. On the other hand,
declarative languages such as Prolog and FormulaOne (which are very high-level languages) have the needed tools
built into their inferences engines.
At the start of the 1990's it is apparent that new development in computer languages has lagged behind hardware
development.
The transition to declarative programming may still be lengthy for the software industry.
Certainly for the individual, time is required to switch over to new languages and to learn the new styles,
philosophies and techniques they require. Complex and flexible applications will require both declarative and
procedural programming. Prolog is the widest known of declarative languages but it suffers from the flaw of
lacking procedural and program control features and must simulate them. FormulaOne has overcome this stumbling
block and has elegantly integrated both programming philosophies into one unit.
FormulaOne can be learned by a beginner but will be most appreciated by experienced programmers.
If you are a problem solver, FormulaOne's truly unique implementation of constraints will be invaluable. Constraints
enable numeric problems to be solved more rapidly, by orders of magnitude - in real time. And they work
readily with FormulaOne's highly structured and modular nature to produce better code. "Better"
code means more readable, more error-free and easier to maintain and change. This is another reason why FormulaOne is superior to any other
declarative programming language.
FormulaOne is a computer programming language, but it's also a complete programming environment that gives programmers
the ability to
efficiently develop, test and run their programs.
At the heart of FormulaOne is the language itself, which can be viewed as a successor to the procedural language of the
third generation
Pascal, extended to cover the paradigms of database languages (fourth generation) and logic languages (fifth generation).
FormulaOne has the readability and efficiency of third-generation languages like BASIC, C, and Pascal, and the database update and query
capabilities of fourth-generation systems.
These features are all brought together by the powers of symbolic computing and logic programming with backtracking search - the same power
as in fifth-generation languages like Prolog.
Along with the FormulaOne language comes a complete visually oriented IDE environment. In the FormulaOne system, users can edit, compile,
and run programs; build, query, and update database files; and create interlocking structures of program modules and databases of
any desired complexity.
FormulaOne and Other Languages
FormulaOne is a new programming language, so it's useful to compare and contrast it to other popular programming languages.
The foundations of FormulaOne are most like those of Prolog. Both languages:
- Are based on mathematical logic, and have a precise declarative semantics (a static, clearly-defined meaning for every
component of the language)
- Have programs which are run by asking questions rather than giving commands;
- Are able to handle symbolic variables, whose values are determined by backtracking search.
- However, FormulaOne recognizes the deficiencies of Prolog in areas where languages like Pascal do better.
Both FormulaOne and Pascal:
- Have a clear but concise nested program structure, rather than the difficult-to-read clauses of Prolog;
- Have if and case constructs that improve readability;
- Can produce fast, compact, non-backtracking code when desired.
But the type structure of FormulaOne is more like that of C than the loose structure of most prologs or the rigid one of
Pascal. In FormulaOne, you can build arrays, structures, lists, and unions which are implemented as efficiently
as they are in C. And as in C, terms of one type can be recast into terms of another type, when possible.
FormulaOne also has many advanced features which are not found in either Prolog, Pascal or C. These include:
- A leading-edge decision procedure for systems of constraints composed of arithmetic formulas, built into the language itself;
- A database file query system which is fully integrated with programs;
- Variable modes, which allow the language to check the data flow in programs for correctness;
- Useful data types not found in most languages, such as relations and injections;
- A module system which supports incremental compilation, linking, and loading of program modules.
In addition to all this, FormulaOne is firmly grounded in its underlying logic. Instead of the non-declarative,
extra logical features of Prolog, like "cut", there are features like "if" which are more powerful, readable, and logically
valid. There is not a single extra logical feature in FormulaOne.
FormulaOne is different from other programming languages, and systems, in
many ways. In well-known languages like Basic and Pascal, we order the computer
to perform some task for us, and watch the results. In FormulaOne, we ask
the computer questions and get responses.
The basic unit of programming in FormulaOne is the formula. A formula is
a statement about the world, phrased in a language similar to mathematical
logic. When we enter a formula into the query window of the FormulaOne system,
it is interpreted as a query; the system will respond by stating whether
the query is true, or by stating the conditions under which it's true.
Simple Arithmetic Queries
The simplest example of a query formula is an arithmetic statement. When
we say 2 + 2 = 4 or x = 3, we are making a statement about the numbers and
variables involved. In general, a formula is a statement, which says something
about objects (like numbers), variables, and the relationships they hold
to one another.
When we type in an arithmetic formula as a query to FormulaOne, we are
asking it to tell us whether the formula is true or false, according to what
it knows about arithmetic. For instance, you can ask FormulaOne whether 2
+ 2 = 4 by the following steps:
The result will be displayed in the window:
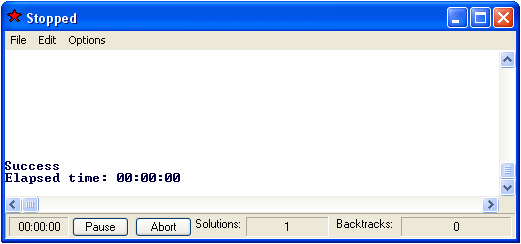
that is, FormulaOne believes it to be true, which is of course correct.
Now try to run 2 + 2 = 5 query instead, it will give us Failure result
instead of Success. After the Success, or Failure comes some statistics
on how long the query took to run.
FormulaOne can tell you whether an arithmetic formula is true or not. But
more importantly, if you pose a query containing variables, FormulaOne will
try to find values for those variables which will make the query true, and
will report to you what those values are. Consider the following example:
The phrase all res indicates to the system that we want to see all the
solutions for the unknown variable we are calling. res::L is a variable declaration;
we can consider it to mean res is a number. The & symbol means and. So
the full meaning of this query is "show all values for res such that res
is a number equal to (3 + 33) multiplied by (4 + 44)".
Instead of indicating Success or Failure for this query, FormulaOne
will give you a solution that looks like following:
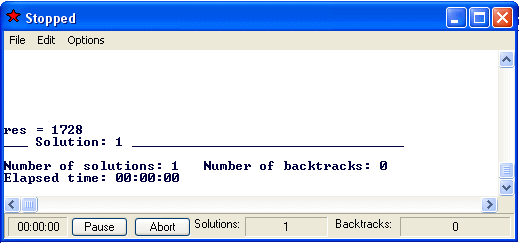
FormulaOne has found one solution to the query, one value for res which
will make the query formula true. That value is 1728, (3 + 33) * (4 + 44).
Actually, you would get the same result even if you omitted everything
in the query up to and including the &. The complete set of circumstances
in which you can do this will be explained later. For now, we will precede
all our queries containing unknown variables with an all phrase and a variable
declaration.
Now let's consider a slightly more complex example.
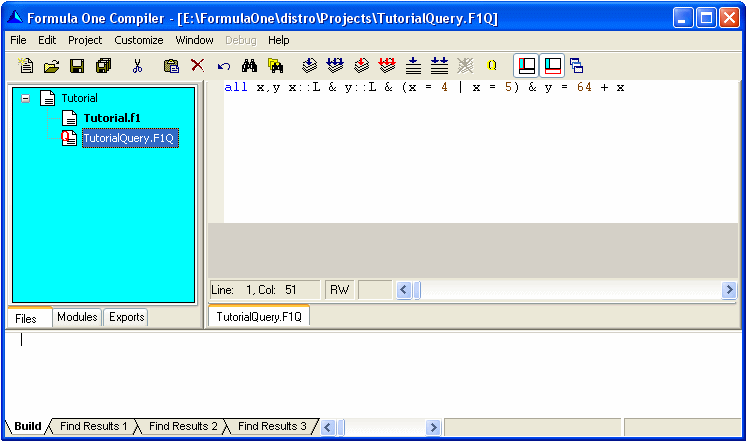
This query has a new symbol, |, which means or. Translation into English
of this query is "show all values for x and y meeting the condition that
x and y are numbers, x is equal to either 4 or 5, and y is equal to 64 + x". You
can see for yourself that this query has more than one solution, and that
the solutions will involve both variables.
FormulaOne has found two combinations of values for the variables, and each
combination satisfies the formula. If we had said all x instead of
all x,y, we would have gotten only the solutions for x, and similarly for y.
If we had said simply all, omitting the list of variables entirely, it
would have defaulted to all variables; that is, the same thing as all x,y.
It's worth noting here that the same solutions would have been found to
the above query if we had said (x > 3 & x < 6) instead of (x = 4 | x = 5).
FormulaOne has considerably more knowledge of arithmetic,
than every other widely-used programming language, including all current
Prolog implementations. It can use this knowledge to figure out that the
first formula has the same effect as the second.
Here are some more examples of arithmetic queries that you can try out:
6*9 = 42
all sec sec::L & sec = 60 * 60 * 24
all f f::L & f-32 = (20 * 9)/5
We can put FormulaOne's knowledge of arithmetic to good use in solving
problems of arithmetic which humans can't solve easily. Consider the following
puzzle.
Some spiders and some beetles are in a box. The box contains forty-six
legs. How many spiders and how many beetles are in the box?
Since we know that spiders have eight legs and beetles have six legs,
we can make a first stab at the puzzle by posing the query:
all s, b s::L & b::L & 8*s + 6*b = 46
We are using s and b to stand for the number of spiders and the number
of beetles, respectively, so 8*s + 6*b must be equal to 46. It seems that
it should work; but when we issue this as a query, the system pops up
the following error message:
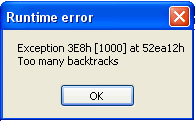
This corresponds to a very large number of solutions (more than 1G).
There are an infinite number of values for s and b because the way we declared
them, they can have either positive or negative numbers as their values.
So because there can't be a negative number of either spiders or beetles,
and the problem indicates that there is at least one of each in the box,
we can add a restriction:
all s::L & b::L & s > 0 & b > 0 & 8*s + 6*b = 46
And now we get the results we wanted, as shown
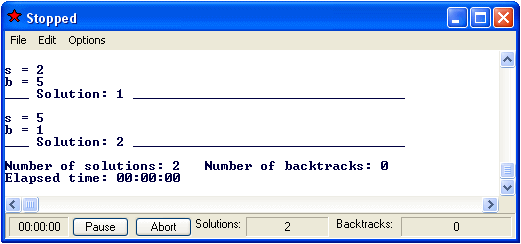
A brief check will show that these are all the combinations of spiders and
beetles that will give forty-six legs in the box. Note the section of the
results screen which states Number of backtracks: 0. This phrase means that
FormulaOne has found these solutions not by trying all possible alternatives,
as all current Prolog implementations would have done, but by applying a
decision procedure for solving arithmetic queries. This decision procedure
avoids having to test the many possible solutions which fail to satisfy the
formula.
Some Formal Definitions
Let's look a little more formally at the syntax of simple arithmetic formulas
and queries in FormulaOne.
-
A variable identifier is:
- a string of letters, numbers, and underscores, starting with a lower-case letter.
A variable identifier cannot be one of the FormulaOne reserved words.
Examples: res, x, fahr_Temp, xyzzy _
- A term can be:
- a variable identifier;
- an integer constant (a string of digits, possibly preceded by a minus sign);
- two terms separated by a +, -, *, / (quotient without remainder), or mod (modulo, or remainder upon division);
- a term surrounded by parentheses, ( ).
Examples: (3 + 33), f + 32, (c*9) mod 5
- A formula can be:
- an expression of the form var::L, where var is some variable identifier;
- two terms separated by a =, <, >, <= (less than or equal to), >= (greater than or equal to), or <> (not equal to);
- two formulas separated by a & (and) or | (or);
- a formula surrounded by parentheses,( ).
Examples: sec::L, 8*s + 6*b = 46, (x = 4 | x = 5)
- A query can be:
- a formula containing no variables;
- a formula preceded by all and an optional list of variables.
This is just a small subset of the whole FormulaOne language. The rest of
this tutorial will be concerned largely with what the "other things", terms,
formulas, and queries can be. A complete and comprehensive description of
the language can be found in the Programmer's Manual section.
We can trust FormulaOne to solve arithmetic queries correctly without needing
to know how it manages to solve them. But when we write programs, we will
have to know more about this, in order to predict the course of events in
our programs. The way it actually solves a query is very complex, but this
section will give a simplified version of the process that will be all that's
needed to understand it.
We'll describe the process using a fairly simple example:
all x x::L & (x<4 | x>6) & x = 10
We'll explain how other kinds of formulas are handled as we get to them.
We can think of FormulaOne as having a query pointer which points to the
current position in the query that it is considering. The query pointer will
be denoted below by the symbol (DownArr). The system will advance the query
pointer through the formula, building up an environment which contains the
information it has so far about the values of variables. Occasionally, it
will set up backtrack points (o) which it will return to if it encounters
inconsistencies. Each backtrack point will be associated with a skip point
later in the query. When the system gets to the end of the query without
getting any inconsistent information about the values of variables, it will
try to print a solution.
- The first thing the system will do is to store the fact that the
user is requesting values of x with the expression all x. Then it will start
the processing of the main part of the query, with an empty environment,
the query pointer at the start of the query formula, and no backtrack or
skip points set up.
x::L & (x<4 | x>6) & x = 10 & (Env: empty)
- The query pointer will be advanced through the first formula, with
the information that x is a number being stored in the environment. The next
formula the system encounters will be an or (|) formula; it will set up a
backtrack point at the or, and a skip point after the second part of the
formula. It will then advance the pointer to the first part of the formula.
x::L & ( x<4 | x>6 ) & x = 10 & (Env: x::L)
- The pointer will be advanced through x<4, with that information
going to the environment. When the pointer reaches the backtrack point, it
will skip over to the skip point. The system is following the rationale that
if 'A or B' is true, we can first assume A, and then come back to B later.
x::L & ( x<4 | x>6 ) & x = 10 & (Env: x<4)
- Now the system encounters an inconsistency. It knows from the environment
that it has assumed x<4, but now it faces the information that x = 10
as well. This is an inconsistency; a failure occurs, causing a backtrack
operation. The system moves the pointer to the last backtrack point set up.
As it does this, it removes the backtrack point, its associated skip point,
and all information that it put into the environment since the backtrack
point was set up. The system is essentially saying 'Assuming x<4 didn't
work after all, so let's try assuming x>6.
x::L & ( x<4 | x>6 ) & x =10 & (Env: x<4)
- Now, the system can advance the pointer through the rest of the query
to the end, without setting up backtrack points or encountering inconsistencies.
When it reaches the end, it will print out the value of x taken from its
environment (as requested by the all clause at the start of the query).
x::L & ( x<4 | x>6 ) & x = 10 & (Env: x=10)
There are no backtrack points set up at the time the pointer reaches the
end of the query, so processing ends there. However, if some backtrack point
had remained, the system would have made a backtrack after printing the solution,
to see if there were more possible solution. It would have kept on doing
backtracks after finding solutions until no backtrack points remained. Figure
2.5 shows the result of this query. Note the Number of fails statistic, which
lists the number of times the system had to make a backtrack due to a failure
(in this case, one, the failure noted in point 4 above). This statistic is
a good measure of how complex the query was to solve. All of our previous
examples have had 0 fails, so they have not been very complicated by FormulaOne
standards.
Queries with explicit or-s in them will always cause backtrack points to
be set up. But implicit backtracks can also occur; for instance, in the query
all x x::L & x > 10 & x < 20
the variable x does not have a single value by the end of the query, so
the system enumerates all the possible values between the bounds that it
knows. It should give each integer between 11 and 19 inclusive as possible
solutions.
Another example of implicit backtracking is the 'spiders and beetles' query
from earlier mentioned earlier. There, the decision procedure for integers caused
a single backtrack to occur which caught the other solution to the puzzle.
That particular example is too complex to go into, but you should be able
to trace through all the other examples without too much
trouble.
The Print Formula
The Print formula is a useful tool for tracing the execution of queries,
and doing simple output to the screen. A formula of the form Print('xxxx'),
where xxxx is any text, can be used anywhere any other formula can. (In fact,
Print is just a predefined predicate in FormulaOne) When the FormulaOne
query pointer is advanced to such a formula, it has the effect of just printing
out the text within the two single quotation marks. For instance, the query
Print('ABC')
will just cause FormulaOne to print the line ABC in the results
window, followed by Success. The query
Print('A') & Print('BC')
would have exactly the same effect, since the Print formula does
not put any space between successive printed text. Other things besides quoted
strings can appear as arguments to Print (the things inside the parentheses).
Any term can be an argument, causing its value to be printed; and if the
special term '\n' is printed, it causes a carriage return.
So the query
Print('ABC\n') & Print((3 + 33) * (4 + 44))
would cause the output
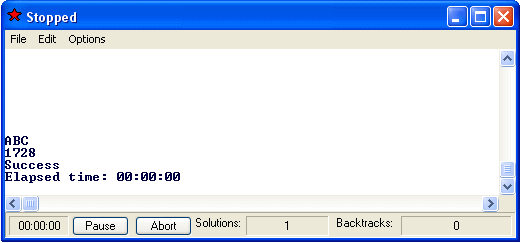
Print arguments can also be strung together within the parentheses, if they
are separated by commas. So the query
Print('ABC','\n',(3 + 33) * (4 + 44))
would have exactly the same effect as the query above.
Print can be used effectively in helping us follow the course of computation
of a formula. Any backtrack that causes a Print to be re-evaluated will cause
the text in it to be printed again. We can insert a Print formula into our
extended example above:
all x x::L & (x < 4 | x > 6) & Print('Here\n') & x = 10
Then the output of the query will look like
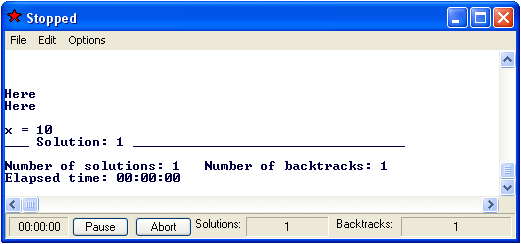
As an exercise, you might want to trace through the execution of this query
just to see that the result above makes sense.
Summary
- The basic unit of programming in FormulaOne is the formula.
- If a formula with no variables is entered as a query, FormulaOne
will tell whether it is true or false; if a formula with variables is entered,
FormulaOne will give values for the variables which will make the formula
true.
- FormulaOne solves a query by stepping through it from left to right,
sometimes skipping over parts of it and coming back to them later through
backtrack operations.
- The Print formula can be used to get the system to print things
on the screen.



Last updated: October 4, 2009